When 27-year-old Dual Degree student Sumit Kumar Jha quietly revealed the publication of not one but three single-author papers during the course of the tumultuous 2020, the research community sat up and noticed. We probed a bit to first learn more about his area of expertise, the genius himself, and discovered what the excitement was about.
The year 2020 has been labelled variously as the year of loneliness, isolation and of course a seemingly endless wait (for the Covid-19 vaccine). But researcher Sumit Jha turned this around to his advantage and nosedived deep into the world of number theory. The result has been nothing short of spectacular: A paper on ‘A formula for the number of partitions of ‘n’ in terms of the partial Bell polynomials’ accepted for publication in The Ramanujan Journal, another on ‘A Combinatorial Identity For The Sum Of Divisors Function Involving pr(n)’ published in The Integers Journal, and yet another on ‘An Identity For The Sum Of Inverses Of Odd Divisors of n In Terms Of The Number Of Representations Of n As r Squares’ published in The Rocky Mountain Journal Of Mathematics.
What It Means
Before engaging in conversation with Sumit, we met up with his advisor Dr. Girish Varma at the Center for Security, Theory, and Algorithmic Research (CSTAR) who helped in deciphering Combinatorics and generating functions. “They are one of the earliest areas of study in the history of mathematics along with Number Theory and Geometry,” says Dr. Varma calling Combinatorics as the science of counting. “It’s something that we often take for granted. However, counting can be very difficult. For instance, consider figures like below (called graphs). It is not difficult to count the number of distinct figures with n circles that are colored differently but highly non trivial to count when they don’t have colors. Figures like these frequently come up in many diverse fields. For example, these might represent an organic molecule in Chemistry, social network relations, a graph pattern in Data Mining and so on.”

Image Credit: Girish Varma (CC BY-SA 4.0).
Mathematicians over the years have developed highly sophisticated methods for counting and using generating functions is the most useful method. “Generating functions is also closely related to infinite sequences that are recursively defined. For example, the sequence 0,1,1,2,3,5, … (first known to be defined in the works of Pingala from 3rd/2nd century BCE; commonly called Fibonacci Sequence), can be defined recursively by F(n) = F(n-1) + F(n-2). It can be shown that F(n) is also the number of different ways one can climb a stairs of n steps taking only 1 or 2 steps at a time,” he says. The proof can be gleaned from the picture below.
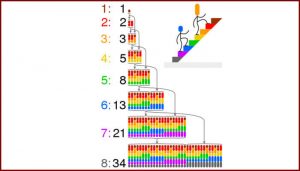
Image Credit: Cmglee (from Wikipedia; CC BY-SA 4.0)
Though a formula for F(n) is known in terms of the golden ratio (See Binet’s Formula), it’s not always possible to obtain in other cases. It is often possible to relate complex counting problems in terms of well understood generating functions like that of F(n). Such formulae are commonly called combinatorial identities.
Number Theory
Sumit on his part attempts to demystify his research work by focusing on his most recent one. And what better start than by drawing attention to the 2015 British biopic on one of the greatest Indian Mathematicians of all time, Srinivasa Ramanujam. Titled ‘The Man Who Knew Infinity’, the central theme of the film revolves around Ramanujam and Cambridge mathematician G. H. Hardy who came up with an approximate formula for calculating p(n), where given any natural number ‘n’, p(n) stands for the number of ways of writing ‘n’ as a sum of smaller (or equal) natural numbers. For instance, there are 5 ways to represent 4 as a sum of smaller (or equal) natural numbers, namely, 4 = 3 + 1 = 2 + 2 = 2 + 1 + 1 = 1 + 1 + 1 + 1. In this case, p(n)= 5. The partitions of numbers from 1 to 8 are expressed diagrammatically below (commonly called Young Tableau).

Image Credit: R. A. Nonenmacher (from Wikipedia; CC BY-SA 4.0)
“The value of p(n) grows very fast,” says Sumit, adding, “The value of p(200) is about 4 trillion, so it is impractical to write down all the ways in which 200 can be written as a sum of natural numbers. How do we calculate p(n) without actually writing all the ways of writing n in this manner? That is what mathematicians are good at doing!”.
Following The Greats
It was in the 18th century that Leonhard Euler first came up with a method of calculating p(n). In 1916, Ramanujan and Hardy approximated a formula for it. And now in an upcoming paper for The Ramanujan Journal, Sumit has shown that the Euler’s method gives a formula for p(n). In addition to this, Sumit has demonstrated that the formula can be generalized for ‘fractional (or colored) partition function’. “Surprisingly, the colored partition function has appeared in the study of quantum black holes and in the area of Statistical Mechanics,” he muses.
Mathematical Mind
Shying away from labels of a Math genius or whiz, Sumit admits that the interest for numbers and Math has persisted since High School. “But I was not very good at it,” he says modestly. The numerical fascination began with the reading of Ramanujam’s first paper on Bernoulli numbers. Incidentally, Sumit’s first Math research paper (and four others) is on Bernoulli numbers. It was when he was pursuing his BTech degree in Computer Science and Engineering at Birla Institute of Applied Sciences, Nainital that he chanced upon a newspaper advertisement of IIITH’s admission process. He applied for a Dual Degree at IIITH under the Lateral Entry programme and was unsurprisingly selected. “The research element of the course attracted me,” he says. Dr. Girish Varma is all praise for him, “Sumit mostly self-trained himself on using combinatorics and generating functions. He gave combinatorial identities relating sequences that are seemingly unrelated. His proofs are short and involve clever manipulations of generating functions.”
Inspiration In Isolation
For Sumit, being at IIIT has given him a lot of spare time to pursue whatever interests him. When taking an academic breather, he can be found listening to music and reading novels on fiction. Ask him about his secret sauce, and he says, “I think doing any research that is mathematical in nature requires a lot of boredom (to fuel the creative juices) and isolation. For someone like me, the lockdown helped with both.” He counts Ramanujam as his single biggest inspiration and credits all his work – 12 papers in all, and counting! – to the methods learned from the great scholar. Quoting Newton, “If I have seen further it is by standing on the shoulders of giants,” Sumit says, “In my case the giant is Ramanujan”. However unlike his idol who credited his capabilities to the presence of divinity, Sumit simply says, ”Unfortunately, I don’t have any such contacts. I merely use the tools he (Ramanujam) and others had developed, which any average human researcher would use.”

Math and Theory at IIIT
Though IIITH is better known to attract and as the center of clever programmers and ML enthusiasts, there is a small but growing community of students interested in Mathematics and Theory. The faculty working in such areas is also growing, with more members expected to join in the coming months. Courses are also being offered on Number Theory, Advanced Combinatorics and Probability.
Special thanks to Dr. Girish Varma for the technical inputs.


